編者薦語
本次推薦的是我院胡安寧教授發於《社會學研究》上的文章《處理效應異質性分析——機器學習方法帶來的機遇與挑戰》
原文刊發於《社會學研究》2021年第1期,原文鏈接🏌🏻♂️:http://shxyj.ajcass.org/Magazine/Show?id=76588
摘要
處理效應異質性是定量社會科學關註的重點🕵️。本文以因果隨機森林與貝葉斯疊加回歸樹為例,指出以算法為導向的新興分析手段可以克服模型形式和變量選擇的限製,並考慮變量間各種交互關系↔️。因果隨機森林與貝葉斯疊加回歸樹分別體現了“匹配”和“模擬”的分析邏輯,以幫助研究者勾勒出異質性處理效應的經驗分布並探索該異質性的決定因素。然而,參數設定差異和算法差異都會損害處理效應異質性分析結果的穩健性👒。
一、問題的提出
社會科學經驗研究往往圍繞變量之間的關系展開。隨著因果推論方法在社會科學領域內的逐漸普及,定量社會科學研究逐漸從強調相關關系轉向強調因果關系(胡安寧😹,2012;Morgan & Winship🙋♂️⚛️,2015)🥷🏻。除了常規的平均因果效應之外🥙🧑🏼🌾,越來越多的學者開始關註處理效應的異質性(謝宇,2008)。這種對於異質性的考察有其社會學基礎🚼🥷🏻。一方面,大量的社會學中層理論都是圍繞特定人群的細分展開的,凸顯了個體間的異質性。這也就不難理解🤦🏽♀️,在驗證和推進這些理論的時候,社會學研究者需要關註處理效應的差異。另一方面👨🏻⚕️,從實踐的角度出發😝,大量的以政策分析為導向的研究關註特定人群之間有差異的處理效應(例如:Heckman & Vytlacil,2001👩🏿🍼;Heckman & García,2017)。這與醫學研究中日漸興起的針對特定類型患者的“精準醫療”存在異曲同工的分析邏輯。顯然👷🏻♂️👲🏼,這類實踐導向的分析要求研究者重視處理效應在不同人群之間呈現出的異質性。
傳統的回歸模型通過交互項來分析處理效應異質性(Aiken et al.,1991)🤸🏼♀️。之後方法論的發展則日漸依托於傾向值(propensity score)的估算,將處理效應異質性問題轉為考察處理效應如何隨著個體傾向值的變化而變化(Xie & Wu,2005;Xie et al.🧷,2012;Carneiroet al.,2010;吳曉剛🧄,2008)。這些分析方法雖然展示了處理效應異質性估計的多種策略🫱🏻,但各有其不足之處。隨著機器學習方法與社會科學因果推斷分析的日漸結合➾,一個前沿的方法論發展方向是使用基於算法的技術手段來考察處理效應異質性。
在此背景下,本文希望能夠通過系統的梳理🐡,展示社會科學研究在考察處理效應異質性時從傳統的線性模型到新近的機器學習算法的方法論發展脈絡,特別關註不同方法之間的優缺點🥡。在此基礎上,本文選取了因果隨機森林(causal random forests)和貝葉斯疊加回歸樹(Bayesian additive regression trees)兩個以非參數“樹模型”算法為基礎的分析技術,具體介紹其算法原理以及如何克服傳統處理效應異質性分析的諸多限製。與此同時🤶🏼,本文也反思了以算法為基礎的新興分析技術可能帶來的潛在問題,如因參數設定差異和算法差異而損害處理效應異質性分析結果的穩健性。這種分析異質性處理效應時出現的穩健性缺失也可以被稱為“異質性的異質性”問題。最後,我們以分析中國精英大學教育回報的異質性模型為例,來展示這些方法論的優勢和不足🥷。
二👩🔬、處理效應異質性的傳統分析:方法概觀
(一)傳統回歸模型的交互項分析
對於處理效應異質性的探索,傳統的分析手段是在某個回歸模型中增加交互項(Aiken et al.😮💨,1991)。如果用Y表示因變量,T表示處理變量🏞,C表示某個可能帶來處理效應異質性的變量,則交互項模型如模型(1)所示,其中我們關心的系數是β3🧚🏿♀️👨。
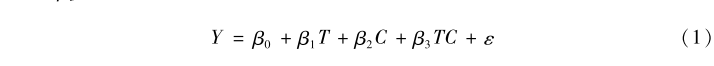
交互項模型雖然使用廣泛,但是相關的方法論研究對其是否能夠準確呈現處理效應異質性一直有所質疑(Hainmueller et al.,2019)。疑問主要來自兩個方面♡:其一,能夠帶來處理效應異質性的因素C可能有很多🎼,但是在給定數據的情況下,我們不可能無限製地在模型中添加大量的交互項。因此🧑🏽🎨,對於交互項的設置便具有一定的主觀性甚至隨意性。其二👐🏿,交互項的具體形式(變量C的二次方3️⃣、三次方項,或者三個甚至更多變量交互的情況)往往也是研究者主觀設定的💆♀️,而這種設定並不必然符合數據生成過程的基本特征。交互關系的復雜性通常不會在常規的雙變量交互項分析中涉及。
(二)以傾向值為導向的處理效應異質性
當傾向值方法逐漸引入定量社會科學研究以後𓀐,對於處理效應異質性的考察便逐漸以傾向值為導向展開(Xie & Wu,2005;Xie et al.,2012)。所謂傾向值,是指個體接受處理變量某個取值水平影響的概率。假設所有的混淆變量(confounding variables)構成矩陣C🛗,那麽🌾,傾向值的估計值就是
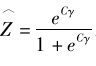
其中γ為矩陣C的系數向量。基於傾向值的此種定義⛎,所謂以傾向值為導向的處理效應異質性分析🧙🏽♂️,就是看處理效應如何隨著傾向值取值的變化而發生變化☺️。
以傾向值為導向的處理效應異質性分析有其獨特的優點🤫。例如🤷🏼♀️,這條路徑不再看某個特定變量C的作用,而是將所有的C降維為一個傾向值Z,進而看傾向值如何異質化處理效應。從這個意義上講,這一方法克服了上述回歸模型交互項的第一個局限。此外⛹🏼♂️,由於處理效應和傾向值構成了一個二維體系🚴🏼,對於它們之間關系的考察也可以突破原有的線性設定🌍,進而采用一些半參數甚至非參數的平滑方法,以應對可能的非線性關系(Keele🧗🏿♀️🤵🏿♀️,2008)🧑🏻🚀👂🏻。這樣🏄🏼,回歸模型交互項分析的第二個局限便被克服了。
具體而言,謝宇和其合作者提出了三種以傾向值為導向的處理效應異質性的分析手段(Xie et al.,2012;Zhou & Xie,2020)。一種被稱為細分—多層次法(stratification-multilevel method)🧎♀️➡️,意指將估算出的傾向值分成不同的取值區間,然後在每個區間內估計處理效應🎤,最後看多個區間的處理效應呈現出何種異質性的變異。第二種方法被稱為匹配—平滑法(matching-smoothing method),即先通過傾向值匹配,計算每個匹配對(pair)的處理效應🧛🏽♂️,之後,對於這一系列的基於匹配對的處理效應進行曲線擬合,考察處理效應如何隨著傾向值取值的變化而變化。第三種方法被稱為平滑—差值法(smoothing-differencing method)。與第二種方法相比,這一方法的特點在於,先分別對實驗組和控製組的個體取值Y隨著傾向值的變化而變化的模式進行曲線擬合👕,之後再看兩條曲線之間的差值,從而得到處理效應異質性的估計。謝宇等人所提出的這一系列以傾向值為導向的處理效應異質性分析方法和經濟學家詹姆士·海克曼提出的邊際處理效應(marginal treatment effect)有異曲同工之妙(Carneiro et al.,2010)。關於邊際處理效應方法⚓️,可參閱胡安寧(2015)🙅🏼、周翔和謝宇(Zhou & Xie🧖🏻♂️,2019)的研究👩🏿,這裏不再贅述👱🏽♀️👑。
以傾向值為導向的處理效應異質性分析雖然突破了回歸模型交互項的一些局限🤼♂️,但也有自身的問題。首先,傾向值的估計存在著模型不確定性和系數不確定性問題(胡安寧,2017)。其次🚏,將各種混淆因素總結為一個傾向值Z的做法雖然通過降維簡化了分析,但是我們也無法具體考察究竟是哪個混淆變量C起到了對處理效應進行異質化的作用。最後,無論謝宇還是海克曼的方法🧓🏿👩🏿🏫,都重在描述處理效應隨著傾向值的取值變化而如何變化,但未能分析是什麽因素造成了此種處理效應異質性。
三⏩、以算法為基礎的機器學習新工具✨:因果隨機森林與貝葉斯疊加回歸樹
按照統計學家利歐·布雷曼(Leo Breiman)的經典劃分(Breiman🍙,2001)🏷,無論是線性回歸模型的交互項👨🏿🌾,還是以傾向值為導向的處理效應異質性分析,都屬於以數據隨機生成(stochastic generation)為分析基礎的模型。這一分析範式需要對統計模型有清晰的設定。與之相應,分析的關註點則放置於模型提供的特定統計量之上(如特定的系數)。與之相比,以算法為基礎的分析工具則對數據生成過程存而不論📡,轉而通過在數據上應用特定算法🧘🏽♀️𓀛,讓數據“說話”,以呈現某種關聯性✷。如果說早期的算法模型因為算力和數據量的限製尚不為社會科學研究者所熟知🏋️♀️,那麽當我們有足夠的計算資源來針對數據使用比較復雜的算法時,我們則不得不正視算法模型在社會科學領域內可能扮演的重要角色🙅🏻。這方面,因果推斷技術與機器學習算法的結合正是當下社會科學方法論發展的前沿方向。在已有的一些探索的基礎上(例如廣義疊加模型[generalized additive modeling]🐢、部分線性模型[partial linear regression]等),湧現了一系列新的適用於因果推斷的算法模型👲🏼。本文針對因果處理效應的異質性,選取了兩個以“樹模型”算法為基礎的分析工具🙇🏽♂️✸:因果隨機森林(Athey et al.,2019;Wager & Athey,2018)和貝葉斯累加回歸樹(Chipman et al.🏠,2010;Hill et al.,2020)。由於這兩個方法都是以樹模型為基礎展開的,這裏首先對樹模型進行概覽性的介紹。
(一)樹模型與隨機森林概覽
樹模型是一系列以數據細分為基礎的算法模型的統稱(Breiman et al.,1984)。如果分析的因變量Y為分類數據,通常稱之為決策樹,而如果分析的Y為連續型變量,則稱之為回歸樹。為了表述方便💘🧘🏽,這裏統稱為樹模型。
一個樹模型如圖1(a)所示,對於數據中的所有樣本,依據某種變量的取值標準,進行不斷的細分,從而構建一個樹形模型(這裏用h指代某一樹模型)。例如,我們首先以變量C1為基礎🐟🦹🏿♀️,以取值0.5為界🥱,如果大於0.5,則將數據分配分到左邊一個樹枝,反之則分到右邊。在右邊這一分支下,依據C2來進行進一步細分,C2大於0.5則到左枝➗,否則到右枝。究竟在分叉處選取哪個變量以及采用該變量什麽數值為界進行細分,都有相應的計算標準(如信息增益比、Gini系數🤸🏼,等等)和算法規則👷🏿♀️,這裏不再贅述。每個樹枝的結尾視為一個節點🤢。如果無法進一步細分(例如,節點內的人的Y取值已經比較近似🙇🏼,或者沒有足夠多的人進行進一步的細分),則每個節點內部所有人Y取值的均值視為符合該節點特征的所有人的Y的估計值。例如,對於C1>0.5的人🧖🏽,估計值為μh1🏋️,對於C1<0.5和C2>0.5的人而言,估計值為μh2,最後對於C1<0.5和C2<0.5的人,估計值為μh3。這種對於數據的樹狀劃分等價於圖1(a)的右圖。
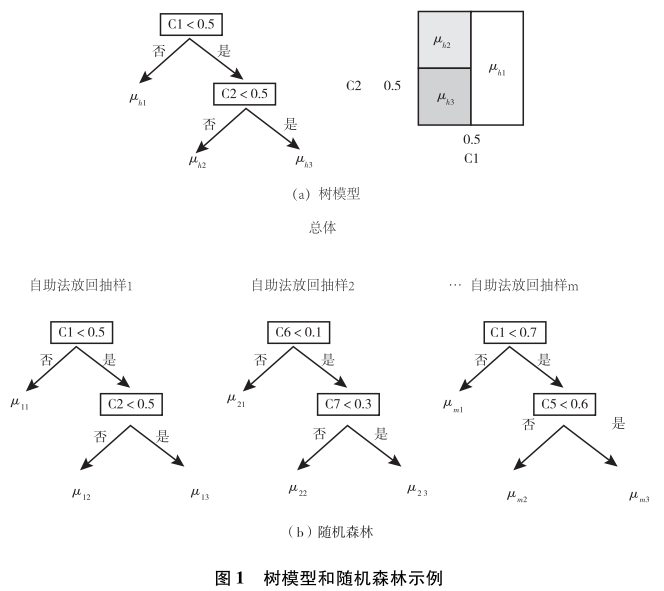
樹模型的問題在於這棵樹可能會很長👐🏼,從而帶來數據的過度擬合問題。為了解決這一問題,一個常用的技術是隨機森林算法,這一算法的邏輯如圖1(b)所示🎲。隨機森林涉及兩個隨機。一個隨機是從分析對象總體中采用自助法(bootstrap)抽樣得到多個子樣本(假設共M個子樣本),之後在每個子樣本中擬合樹模型。另一個隨機是在每個樹模型的分叉點🤲,采用的分叉變量是從所有的備選變量中隨機選取產生的👩🏻🏫。例如❕,在圖1(b)中,第一個樹模型用到的變量是C1和C2👊🏻,第二個樹模型用的是C6和C7,第m個樹模型用的變量是C1和C5。在得到M個樹模型之後,對於某個個體,基於其一系列的背景特征💥,我們可以得到M個對於其Y值的估計值。假設某個個體的取值為C1=0.6♎️,C2=0.2,C5=0.3🎆,C6=0.8,C7=0.2,則在第一棵樹下,其Y的估計值為μ11,第二棵樹下的估計值是μ21🫶🏿,第m棵樹下的估計值是μm3。如果Y是一個連續型變量,我們就可以計算這m個估計值的平均值🙆,從而得到對於Y的整體估計
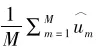
如果Y是一個分類變量⛪️,那麽我們可以采用投票的方式(例如服從多數原則)決定Y的整體估計值🏔。
(二)因果隨機森林
因果隨機森林可以看作是隨機森林算法在因果推斷問題上的直接應用(Athey et al.,2019🈴;Wager & Athey🙋🏽♂️,2018)👵🏽。這一方法的基本目的是最大化處理效應在不同樹模型節點之間的變異👷🏼。具體而言,因果隨機森林和傳統隨機森林方法相比,在節點分叉、模型擬合和處理效應估計三個方面都有自己的特點。
節點分叉。我們用P表示母節點,其分叉為左右兩個子節點C1和C2。那麽⤵️🙍🏿♀️,在傳統的樹模型中,我們判斷是否繼續分叉的依據可以是分叉後每個子節點內部對Y的估計誤差。例如🏀🎞,假設兩個子節點C1和C2對Y的估計值分別為μ^c1和μ^c2👜,其樣本量分別為nC1和nC2🪖,處於兩個子節點中分析對象Y的觀測值分別表示為YC1和YC2,則兩個子節點的估計誤差分別為
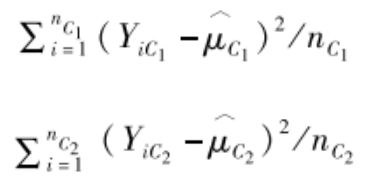
那麽,如果C1和C2中個體人數比例分別為
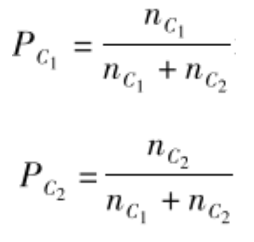
那麽節點分叉後的總誤差為:
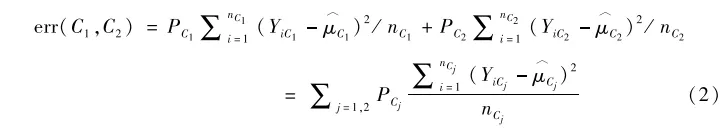
從方差分析的角度來看,上面的分叉標準實際上是要求組內方差最小化。與之相比,因果隨機森林則在每個節點內估計因果效果τ^c1和τ^c2(如每個節點內部實驗組的Y的均值減去控製組的Y的均值👩。當然,這裏需要保證每個節點內部有實驗組和控製組的個體,詳見下面的參數設置)。此時在決定節點是否繼續分叉時,所采用的標準就不再基於節點內部方差最小💾🧑🦲,而是節點間變異最大,即希望以節點之間因果效果的彼此差異最大化𓀙。順著這一思路🆙,因果隨機森林的節點分叉標準變成了最小化下面的誤差表達式:
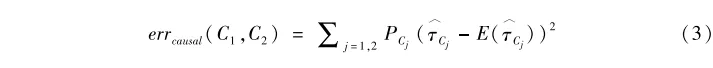
其中,E(τ^Cj)表示不同節點處理效應的期望值。對於這一誤差表達式,經濟學家蘇珊·阿西(Susan Athey)等人證明
errcausal(C1,C2)=常數項-+隨機擾動項。
所以,我們最小化errcausal(C1,C2)等價於最大化
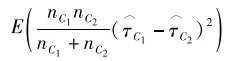
即節點之間估計的處理效應彼此差異盡可能大。顯然🥒,這實際上就是處理效應的異質性。
模型擬合。和傳統隨機森林相比,因果隨機森林在模型擬合方面可以選擇所謂的誠實(honesty)算法。在傳統隨機森林算法中🐛🛌,數據分為訓練組(training)和測試組(testing),其中訓練組用來建立一系列的樹模型和估算節點中Y的估計值û🥙,而測試組則是用新的數據來對模型進行應用(如計算新來人員的û)。但是在因果隨機森林中,誠實算法要求構建樹模型和估計τ^分開進行。也就是說🏄🏽♀️,訓練組數據進而分為兩部分,一部分用於構建樹模型(仍舊稱為訓練組)👨🏻🦲,一部分用於計算節點內部的處理效應τ^(可以被稱為估計組)🟡🪆。這樣做的好處在於減少τ^的估計誤差。在實際操作中🫑👫,研究人員可以自行選擇是否采用誠實算法🙋♀️。這是因為盡管誠實算法有其優勢👨🏽🍳🧑🏼🦳,但是在使用的過程中,訓練組數據要分割使用,因此會壓縮樹模型的訓練數據集。
處理效應估計。基於一系列的樹模型(或者森林),最後一步是對處理效應進行估計。如果有新的觀測對象(即沒有用於樹模型擬合和û估計的新的數據)🖕🏼,基於其背景特征C,我們可以用因果隨機森林來估計某一處理變量對於這一觀測對象的Y的處理效應。具體而言,對於這個新的分析對象i🙍🏿,我們可以根據因果隨機森林中一系列的樹模型計算訓練組中的所有數據點和i同分到一個節點的頻數。頻數越高的人(如個體j)和個體i的背景越接近,自然我們就應當在計算針對i的處理效應的時候給j更大的權重。如果沒有新的測試數據,可以采用包外(out-of-bag)估計來計算權重。
(三)貝葉斯疊加回歸樹
與因果隨機森林相比,貝葉斯疊加回歸樹雖然也是基於樹模型算法的分析技術,但在對樹模型的使用上有其獨特之處(參見Chipman et al.,2010🍴;關於該方法的系統梳理,參見Hill et al.,2020)。為了理解貝葉斯疊加回歸樹,我們首先來看什麽是疊加回歸樹。顧名思義📿,疊加回歸樹將Y的預測值寫成多個樹模型的疊加。如上文所示🏌🏿👵🏻,一個樹模型涉及輸入信息X(處理變量和各種混淆變量構成的矩陣,即X是由T和C構成的矩陣,X=[T,C]),建構的樹Tree,以及節點輸出μ。為了表述的方便💔👨🚀,我們可以用函數g來將三者結合起來🧓🏻,寫為g(X,Treeh,Mh)🔓,其中下標h表示第h個樹模型。基於這些信息,我們可以把Y的估計值Y^寫成如下疊加回歸樹的形式:
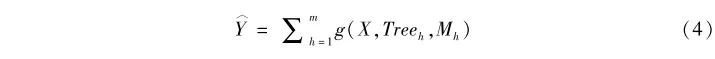
其中🧏,一共有M個樹模型,每個樹模型用Treeh表示☔️,而Mh=(μh1,μh2,…,μhI)’指代每個樹模型的節點處對於Y的預測值。基於這種設定,我們可以把觀測值Y寫成疊加模型的形式🙇🏻♂️📡。假設ε是服從均值為0、方差為σ2的隨機擾動項,我們有:
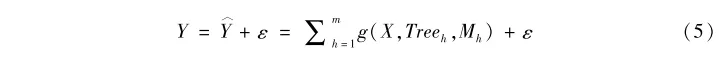
至此🧍🏻♂️,我們建構了一個疊加模型👨🏽🎤。而貝葉斯疊加回歸樹提供了針對它的估計方法。這個方法的優點在於通過調控各種參數先驗分布的特征來控製潛在的過擬合👍。實際上,疊加樹模型非常容易出現過擬合♠️💇。例如👩🏼🏫💂🏿♂️,先擬合樹模型Tree1,之後計算Y減去Tree1得到殘差e1,然後再對e1擬合Tree2🔖,然後計算扣除Tree2後的殘差e2,並針對e2擬合Tree3😋,依次類推。可見,只要樹模型的數量足夠多,結構足夠復雜,必然會對數據過擬合。而引入貝葉斯的先驗概率則有效地控製了這種過擬合情況🧑🏼🍼。
具體而言,在上述模型中一共有三個參數:Treeh,Mh和σ2✧。貝葉斯疊加回歸樹通過分別對它們設定先驗概率保證每個g(x,Treeh,Mh)都是一個弱學習器🫱🏼。正是因為如此,這些先驗概率也被稱為正則(regularization)先驗。具體而言,貝葉斯疊加回歸樹設定σ2服從反伽馬分布,這一分布的均值設為Y的觀測數據的標準差σ^。但是這個參數需要進行一定的數學變換以保證P(σ<σ^)=0.95。每個樹模型Treeh的先驗分布設置為α(1+d)-β⚆,其中α取值在0到1之間,β>0,d表示的是一個樹模型的樹深度(depth),即從頂點到最下面一個節點經過多少分叉。通常我們取α=0.95,β=2,由於-β是一個負值,這一先驗分布使得結構非常復雜的樹模型出現的概率很小。即樹模型越復雜,出現概率越小👩🏻🦽➡️。對於Mh🤦🏿♀️👩✈️,貝葉斯疊加回歸樹設定節點的一系列對Y的估計值服從正態分布🚃。假設某個樹模型下有t個節點👍🏼,則設定μht服從均值為0、方差為ω2的正態分布。對於這一正態分布,設定ω=0.5/k√M♕。其中k可以取值為2,M為樹模型的數量👩🦲。可見,樹模型越多,ω2越小,μht的分布越集中於均值0。也就是說,很多μht的取值會被強製接近於0,從而控製了單個樹模型的影響力,抑製過擬合。最後🏊♂️,和一般的樹模型一樣🖖🏻😺,樹模型分叉處選用的變量和其取值界限的選擇均設定為均勻分布。
在完成上述先驗分布的設定後,貝葉斯疊加回歸樹的估計就進入到傳統的馬爾科夫鏈-蒙特卡洛計算過程,以模擬後驗分布🌴。具體的技術細節這裏不再贅述,具體參見戈爾曼等人的著作(Gelman et al.,2013)💆🏼♂️。基於後驗分布🛶,我們可以通過改變自變量T的取值,模擬T在不同取值下Y的變化,以此估計出處理效應。例如,對於個體A,假設其X取值為[1,C]。那麽,個體A在T=1時的Y的觀測值Yobs即為其在實驗組時的Y值,我們可以利用貝葉斯疊加回歸樹來模擬當個體A的T取值為0的時候Y的估計值😡。例如⛽️,我們可以把個體A的T值強製賦值為0,並將其作為一個新的觀測樣本放入貝葉斯疊加回歸樹(X設置為[0,C])🛥,得到的預測值Y^即為當個體A在控製組時的Y的估計👩🏻🦲。那麽,對於個體A而言,其處理效應為Yobs-Y^。
(四)樹模型的可解釋性:變量的重要性指標
對於定量社會科學經驗研究而言,學者們非常重視模型的“可解釋性”。在因果推斷研究中💕🧑🏻🏭,處理變量和因變量的定義非常明確🕚。因此,模型的可解釋性往往落腳點在如何理解控製變量(或者稱為混淆變量)在估算因果關系過程中的作用(Molnar,2020)。對於樹模型而言,由於在每個樹分叉節點處需要對各個混淆變量逐一“掃描”📠,那麽多個樹節點下,有的混淆變量就會被使用很多次🤌🏽,而有的混淆變量被使用的次數更少🏰👩🏽🏫。這種使用次數的差異本質上代表了某一個混淆變量對於某一因變量的“解釋”能力🚵🏿🫚。解釋能力越高,被用來進行節點分割的次數就會越多。那麽我們就可以看多個樹模型下💩,哪些混淆變量更受“重用”👩🏽🍼,從而了解不同的混淆變量跨越多個樹模型的整體“重要性”程度。在機器學習文獻中,這種混淆因素的重要性也被稱為特征重要性(feature importance)。
這裏需要指出的是,混淆變量的特征重要性🟪,在因果隨機森林和貝葉斯疊加回歸樹這兩個模型之間有不同的含義💂🏿:貝葉斯疊加回歸樹進行的是傳統的樹模型擬合🤓,混淆變量的作用在於在每一個節點處提升因變量Y在子節點內的“純度”,而因果隨機森林則要求每個節點處選取的混淆變量可以提高子節點彼此之間因果效應估計上的差異。換句話說🔊,貝葉斯疊加回歸樹中重要的混淆變量是那些能夠最大化區分因變量取值的變量,因果隨機森林中重要的混淆變量是那些能夠區分處理效應的變量。這種特征重要性定義上的差異需要特別註意🛶。
四🎀、新工具、新機遇、新挑戰
與傳統回歸交互項和以傾向值為基礎的處理效應異質性分析不同,無論是因果隨機森林還是貝葉斯疊加回歸樹,都是基於更為復雜的樹模型算法對數據進行處理的🤌。這兩種方法為我們提供了估計處理效應異質性的新工具💂🏼♂️。基於其方法特點👨❤️💋👨,它們為定量社會科學研究者提供了新的機遇,也帶來新的挑戰𓀗。
(一)新機遇🧑🏽🏭:個體處理效應的趨近及其應用
與傳統的方法相比,因果隨機森林和貝葉斯疊加回歸樹的一個優勢在於,可以為我們提供對個體處理效應的趨近(approximation)估計。眾所周知🐴,因果推論過程中的一個基本問題是我們無法同時觀測到一個個體的觀測值與反事實(counterfactual)值(Holland😢,1986)。也正是由於這一點,常規的因果推斷技術往往估計的是特定群體的“平均”處理效應,而不是個體處理效應🏌🏼♂️。
雖然反事實狀態難以直接觀測,但我們可以將其看成是一個缺失值並填充之(Ding & Li🧆,2018)👱🏿♂️。換句話說,我們只需要通過某種手段把反事實狀態這一缺失值填補進去🧙🏿♀️,然後與觀測到的事實狀態相減就能夠獲知個體處理效應的一個估計👨🏻🎤。順著缺失值填充的思路,現有文獻提供了兩種策略👩👧🧒🏻。一種策略是“匹配”🩸,即盡可能尋找那些與被研究個體接近、但是T取值不同的分析對象來進行匹配(Stuart,2010)💻。另一種策略是“模擬”(Abadie & Imbens🫗,2011)📷。其思路是盡可能地擬合一個完備的針對因變量Y的模型。通過這個模型,我們可以知道,究竟是哪些因素能夠影響Y以及如何影響🤦🏻♀️✋🏽。個體A只要服從這個模型,那麽只需要改變個體A的T取值,就能夠近似地估算出個體A的反事實狀態。換句話說👨🏿🦲,T取值不同時Y的取值差異可以用來趨近個體處理效應🌳。
通過上面的方法論介紹不難發現🌙,因果隨機森林采取了“匹配”的策略。通過生成不同的樹模型👡,訓練組中的每個個體都獲得了一個權重⏬,代表了在各個樹模型中與我們關心的個體出現在同一個樹節點內的概率🧉。由於劃分到同一個節點的個體在大量的混淆變量C上取值相同🔛,因此這一權重本質上反映了訓練組中的個體與我們關心的個體的接近程度,或者說匹配度🧛🏿♂️。權重越大✍🏻,與我們關心的對象越相像,就越能夠影響個體處理效應的估計💭。與之相比,貝葉斯疊加回歸樹則采取了“模擬”的策略。通過貝葉斯方法↪️,我們基於先驗分布的參數值設置可以獲取一系列參數的後驗分布,即疊加回歸樹的基本分布狀態🦂。那麽🏄🏿,我們如果想估計個體A的個體處理效應🎒,只需要將個體A的信息代入,讓疊加回歸樹估算個體A的T在取值不同時的Y的期望值並相減之,由此就得到了個體A的個體處理效應估計。其分析過程的依據在於存在一個訓練得很好的疊加樹模型,以供我們“模擬”出反事實的取值🦖。
那麽,利用因果隨機森林和貝葉斯疊加回歸樹來趨近個體處理效應🟥,對於處理效應異質性的分析有何價值呢👉🏿?首先🚶♂️🏂,因果隨機森林和貝葉斯疊加回歸樹都是基於算法建構樹模型的。因此🍨,這兩個方法盡可能地避免了對於模型形式的人為設定和幹擾。這就在一定程度上突破了回歸模型交互項以及以傾向值為導向的處理效應異質性考察在模型形式上的限製😵。其次,樹模型的建構過程(如設置分叉點)不斷地對混淆變量取值的組合進行考察(T除外),因此,因果隨機森林和貝葉斯疊加回歸樹的一個特點在於幾乎可以窮盡處理變量T和各種其他混淆變量之間的交互關系👧🏻。這種對於交互關系的窮盡是傳統處理效應異質性分析方法無法完成的。最後,個體處理效應的估計值可以成為進一步分析的對象。如上文所述,傳統的回歸模型交互項和以傾向值為導向的分析重在展示而非解釋異質性。與之相比🦈,因果隨機森林和貝葉斯疊加回歸樹幫助研究者估計某個處理變量在“每個人”身上的處理效應大小🍚。那麽🏬,我們自然可以進一步看🧑🎓,究竟是什麽因素影響了這種個體間的差異🧑🏿🦳,從而“解釋”了處理效應異質性。
(二)新挑戰:異質性的異質性
雖然因果隨機森林和貝葉斯疊加回歸樹通過趨近個體處理效應為我們考察處理效應異質性提供了新的思路,但這兩種方法也給經驗研究者帶來了新的挑戰▶️。這個挑戰我們稱為“異質性的異質性”(heterogeneity of heterogeneity)🧑🏽🦱:前一個“異質性”是指對處理效應異質性的估計,後一個“異質性”指的是這種估計會因為算法出現經驗結果彼此不一致的情況。
具體而言📬,造成異質性的異質性現象的原因有二🫧。一方面,與傳統的統計分析相比,基於算法的分析手段需要對更多的算法參數進行設定。雖然基本上大多數的算法模型都提供了默認值👨👧👧,但是此種默認值並非基於具體問題設定😺🦆,因此無法保證普適性。在這種情況下,不同的研究者可能會有不同的參數設定偏好🦹♀️。其結果便是,即使分析同樣的問題,也有可能因為算法參數設定不同而出現分析結果的差異性。另一方面,分析結果還有可能因為算法本身的不同而出現差異。在以機器學習為基礎的各種分析技術中,相較於傳統模型💛🐳,算法被推到一個非常重要的地位。在非學術研究的商業應用中,甚至有算法霸權一說(奧尼爾,2018)。盡管目前在社會科學領域內談算法霸權似乎為時過早,但是算法無疑是決定經驗結果的一個重要因素,而不同算法的差異則有可能成為造成經驗結果異質性的重要原因🛌🏿。
五、經驗示例
(一)研究問題與數據
本文的經驗示例分析了中國精英大學教育回報的異質性💅🏼💼,即與一般大學相比,進入精英大學學習的收入回報在不同個體之間是否以及如何呈現出異質性特征(Hu & Vargas👰,2015)。數據來自於“首都大學生成長追蹤調查”(Beijing College Students Panel Survey🪑,BCSPS)。這一數據提供了大量學生進入大學之前的背景信息🤸🏿,這些信息構成了研究中的潛在混淆變量,從而有助於抑製潛在的選擇性誤差。此外,由於是追蹤數據👨❤️👨,我們在後續調查中獲取了大學生畢業後的初職收入信息🤴。在下面的分析中👴🏻,精英大學選取的是北大、清華和中國人民大學三所大學🏣,這三所大學構成了BCSPS調查三個獨立的抽樣框🤐,因此保證了足夠的樣本量。首都大學生成長追蹤調查的相關信息可以參閱吳曉剛(2016)🧎🏻♀️➡️。
(二)變量選擇
下面分析的處理變量為是否畢業於清華、北大或者人大(1=是,0=否),因變量則是初職月收入水平。除了這兩個變量之外,我們還考慮了其他潛在的混淆變量,包括性別(1=女☑️,0=男),民族(1=漢🛴,0=少數民族),年齡,是否高中復讀(1=是,0=否),目前所在年級(1=大學一年級🌖,3=大學三年級)🦶🏿,家庭年收入(log轉換),兄弟姐妹數量,父親教育水平(1=未受過正式教育,2=小學,3=初中👵🏻,4=高中,5=職高/技校,6=中專👉🏼,7=大專,8=本科,9=研究生及以上),母親教育水平(1=未受過正式教育,2=小學🏰,3=初中🚡,4=高中,5=職高/技校,6=中專📈,7=大專,8=本科🎞🏊🏼♀️,9=研究生及以上),父親是否黨員(1=是,0=否),母親是否黨員(1=是🌙🤲🏿,0=否)👭🙂↕️,父親是否全職工作(1=是,0=否)🚣♂️,母親是否全職工作(1=是,0=否),高中中學等級(1=全國重點中學,2=省重點中學,3=地市重點中學,4=縣重點中學🦹🏼♀️,5=非重點中學)以及入學前的所在地區(1=東部省份,2=中部省份,3=西部省份)。
(三)傳統分析方法的結果
如上文所述🚵🏻♂️🫳,我們研究與一般大學相比,精英大學對於收入的影響異質性。我們首先看精英大學的收入回報異質性是否和進入精英大學的概率(傾向值)相關(Brand & Xie🤞🏽,2010)。在表1中,模型I利用一系列的背景變量擬合了logistic回歸模型。基於此模型,我們進一步估計每個分析對象的傾向值。模型II建立了最小二乘回歸(OLS)模型💆🏻,並考慮處理變量和傾向值的交互關系。結果表明⏏️,精英大學的收入回報與傾向值的交互並不顯著🫄🏼。因此🍫♉️,僅就回歸模型交互項來看,不存在處理效應隨著傾向值變化而變化的情況。
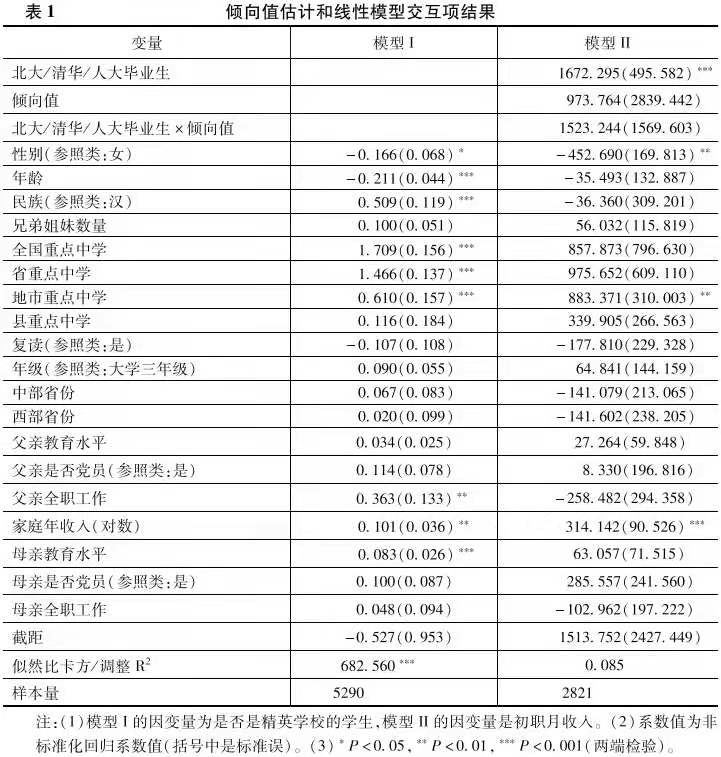
圖2展示了謝宇等人的三個處理效應異質性分析方法以及海克曼的邊際處理效應模型的結果。細分—多層次法說明存在明顯的正向選擇效應🧖🏻,即越容易進入精英大學的人,其教育回報越高(斜向上的趨勢)👨🏻🎨。但是,如果看匹配—平滑法和平滑—差值法的分析結果,則沒有明顯的異質性處理效應🪔。最後,邊際處理效應的結果也支持了正向選擇效應的結論(橫軸是阻礙變量👈,其與傾向值含義相反)🙅🏽。
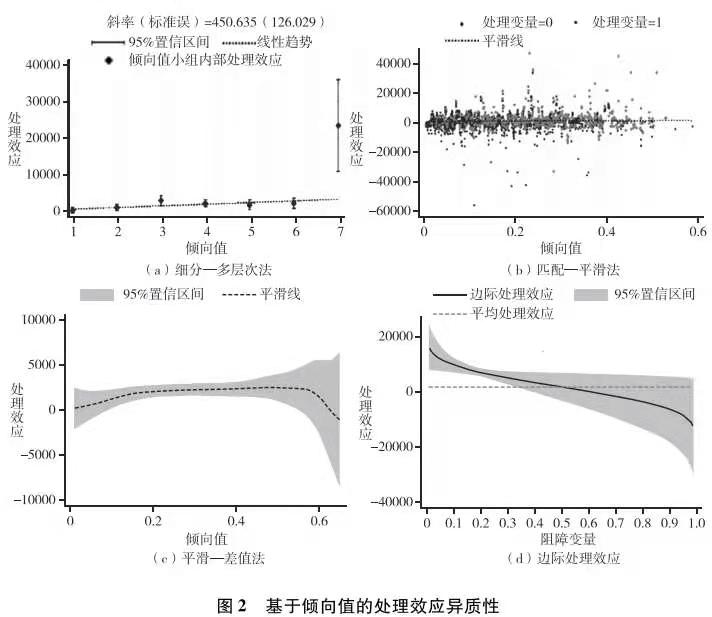
綜上所述👋🏽,回歸模型的交互項⛹🏼♀️、匹配—平滑法和平滑—差值法的分析結果都沒有提供證據來支持處理效應的異質性,但是細分—多層次法和邊際處理效應分析都顯示出一定的處理效應異質性。這種差異本身體現了不同的分析方法對於分析結論的影響。那麽,如果基於個體處理效應的趨近,我們能夠得出什麽結論呢?下面我們就分別采用因果隨機森林和貝葉斯疊加回歸樹進行分析🏘。
(四)個體處理效應的趨近及其使用
利用因果隨機森林和貝葉斯疊加回歸樹可以估計出個體處理效應。我們這裏采用核密度分布勾勒其基本分布狀態🙆🏽👨👩👧👦。我們的帶寬為115,核函數用的是常見的葉帕涅奇尼科夫(Epanechnikov)核函數。以某一觀測值為中心,這個核函數規定了權重在左右兩邊呈拋物線狀下降💅🏼👩🏽🦲,並服從公式0.75×(1-x)2。對於我們分析的樣本🏊🏽♂️,兩種方法得到的處理效應的核密度分布如圖3所示👩🦯➡️🙇🏽。
圖3呈現三個特征。其一,兩個分布基本上重疊,且形狀近似↙️,這說明通過因果隨機森林與貝葉斯疊加回歸樹估計出的個體層次上的因果效果具有比較高的一致性。其二,兩個分布的最高點彼此不同。落實到X軸上,可以看到貝葉斯疊加回歸樹的“眾值點”(分布峰部對應的X軸取值)大於因果隨機森林的“眾值點”#️⃣🫐。因此,二者的估計在最有可能出現的因果效應值上有所不同✦。第三,兩個分布顯示出比較明顯的數據離散度。這說明👩🏿🏭,同樣是考察精英大學的收入回報🤌🏽,處理效應在人和人之間存在很強的異質性。
那麽,為了得到這些估計📗,哪些混淆因素比較重要呢?為了回答這一問題,我們展示了混淆變量的特征重要性指標👨🏿⚕️,如圖4所示⏮。
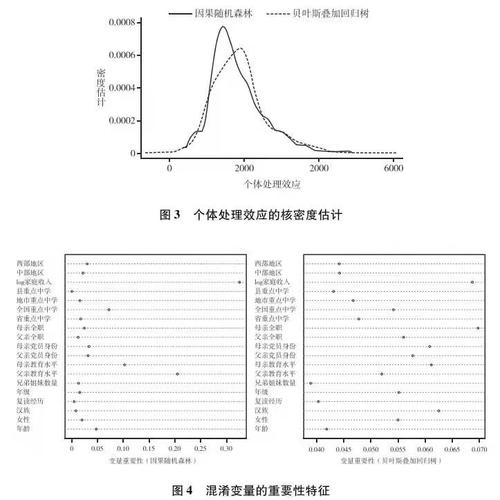
在兩種方法中👩🏿🍳,家庭收入均是一個關鍵的混淆變量🚵。但是對於因果隨機森林而言,次重要的混淆因素是父母的教育水平,但是在貝葉斯疊加回歸樹中,次重要的混淆因素是母親是否全職和是否為漢族🚟。如上文所述,混淆變量的重要性在兩種方法之間存在定義上的差別👷🏼,因此這種經驗結果上的差異可以理解。需要指出的是👩🦲,我們也計算了兩種方法下混淆變量重要性排序的斯皮爾曼排序相關系數(ρ),結果發現,在兩種方法下不同混淆變量的排序具有較高的相關性(ρ=0.36;P=0.137)。這說明,盡管在不同方法下混淆變量重要性指標的定義有所不同,但整體而言🤝🧗🏻♂️,各個混淆變量的重要性順序具有較高的一致性。
基於個體層次的處理效應估計,我們可以直接用散點圖來觀察處理效應如何隨著傾向值的變化而變化。相關的結果參見圖5。無論采用哪種分析方法,其估計出的個體處理效應都和傾向值之間存在正向的聯系(P<0.001)👨🏼🎨。即,精英大學的回報隨著進入精英大學概率的增大而增大💎,即存在某種正向選擇效應🏃➡️。
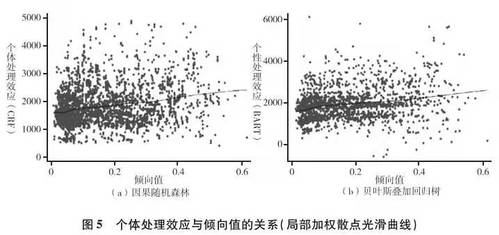
下面,我們可以進一步探索哪些具體的混淆變量能夠影響處理效應異質性🏃🏻♂️➡️。OLS模型的分析結果參見表2。其中🌬,兄弟姐妹數量、父親教育水平和家庭收入的提升可以顯著提升個體處理效應。這在一定程度上說明🤦🏽♀️,出身良好家庭背景的個體進入精英大學,其從大學教育經歷中獲得的回報相比於出身一般家庭背景的個體更高。但是來自全國重點中學的精英大學學生的回報反而偏低🦹🏻♂️,這或許與樣本選擇效應有關(例如,全國重點中學的學生有相當一部分高中畢業後選擇出國而非留在國內讀書,或者他們在國內精英大學畢業後更傾向於繼續深造而不是立刻工作🧎🏻。此時,立刻進入勞動力市場的精英大學畢業生或許並不是那些最能夠從勞動力市場獲取高收入的群體)。除了這些變量,母親教育水平和全職工作雖然在兩個模型中都是顯著的🥷🏿,但是估計的效應相反👩🦳🙍🏽♀️。
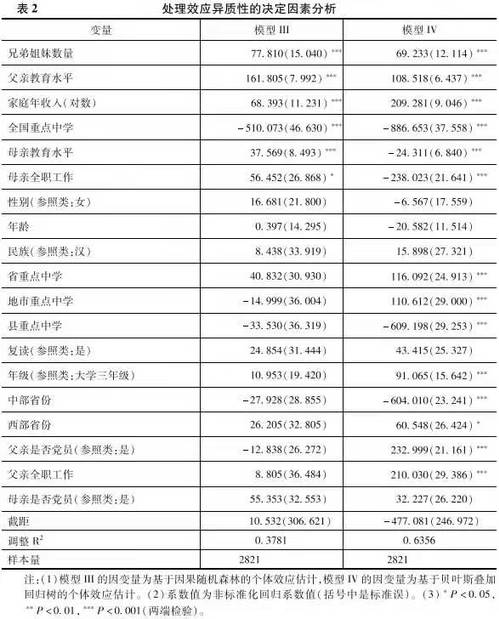
上面的分析結果顯示了兩種分析方法彼此之間的差異。例如,對於個體層次的因果處理效應估計,基於貝葉斯疊加回歸樹的分析結果表明👃🏻,諸如學校等級↖️🧝🏻、年級👩🏿⚕️、省份😿、父親是否黨員以及工作狀態這些混淆變量都有顯著的相關性。但是基於因果隨機森林的分析結果沒有展示出類似的經驗模式👩🏻🦱。這種差異或是不同的算法邏輯所致,關於這一點⚽️🥥,下文對於“異質性的異質性”的分析將進行討論。除此之外🚵♂️,另外一個可能性在於數據量的限製。基於算法的分析技術往往需要“海量數據”的支撐,以便有足夠的信息進行模型的訓練。因此🚏,本文2821的數據量對於訓練因果隨機森林和貝葉斯疊加回歸樹而言或許不夠。如果是這樣的話,那麽訓練出的模型有可能不夠精確,從而帶來了因果隨機森林與貝葉斯疊加回歸樹之間的差異⚆🧢。我們這裏借助自助法(bootstrap)的思路來檢驗一下數據量大小的潛在影響👨🏻🦲。具體而言,我們采用放回抽樣的方式🧜🏻♀️💂🏿♀️,以原始的首都大學生成長追蹤調查數據為基礎,生成了一個10萬樣本量的新數據。分析發現,即使我們把樣本擴充到10萬🎥,不同的方法所估計出的個體層次處理效應與混淆變量的關系依舊呈現明顯的方法間差異。基於這一發現,我們可以初步認為😮😯,上面呈現的經驗結果差異應當主要歸因於不同方法之間的差異🎐,而不是樣本量問題🧥。
(五)異質性的異質性
在展示了以機器學習算法為基礎的方法優勢之後🟩,本部分將著重展示“異質性的異質性”對研究者提出的新挑戰。我們首先考察內部的異質性🦄,通過調整算法基本參數,看經驗分析結果的變異度(上面的分析基於參數的默認取值)👩🏻🎨。針對因果隨機森林,我們先後擬合基本模型(各種參數設為默認值)👨💻、變量選擇模型(基於隨機森林的變量重要性指標,僅保留重要性大於所有變量重要性均值的變量)🏋🏿♂️、誠實算法模型(采用誠實算法如果采用誠實算法,那麽我們在訓練數據中再將其中50%用於樹的分叉設置👰🏻,50%用於填充數據。即在所有樣本中,25%(即50%×50%)用於分叉,25%用於數據填充。)和不同樣本比例模型👯。樣本比例是指在總樣本中用於訓練樹模型的訓練組樣本所占的比例,這裏先後設置為30%、20%和10%。這樣👩🏻🦯➡️,對於因果隨機森林📤,我們一共有六個基於不同算法參數的模型,其個體處理效應的估計分布及其相互關系如圖6所示🟦。
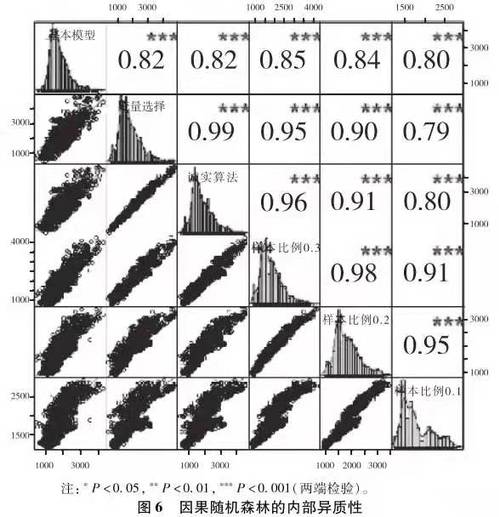
通過圖6可以發現,盡管不同的模型參數設定下的個體處理效應分布有些許差異🍬,但整體而言,不同的參數所估計出的結果之間有著比較高的相關性(相關系數如右上角的數字顯示,取值區間為0.79-0.98,且均統計顯著)👮🏽。因此,因果隨機森林呈現比較低的內部異質性🧝🏿♀️。
如上述討論,貝葉斯疊加回歸樹的主要的參數是樹模型的數量☝️。其中默認的是200🔹。除了這一基本模型外🧑🦲,我們先後擬合了5個、10個、50個🤦🏻、100個和500個回歸樹的貝葉斯疊加回歸樹模型。其對於個體處理效應的估計及其相互關系如圖7所示。
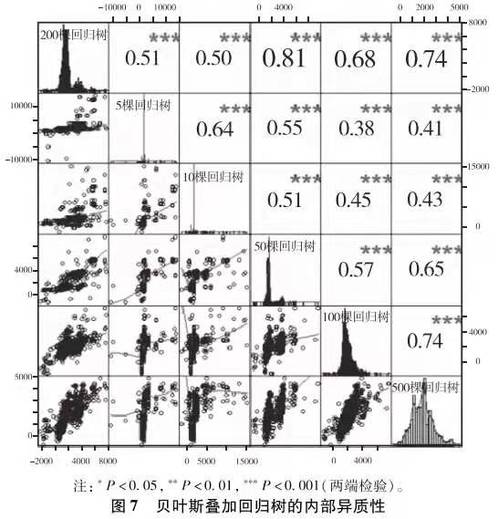
顯然,貝葉斯疊加回歸樹的內部異質性程度很高👋🏼🪝,盡管相關系數都統計顯著☔️,不同的參數設定估計出的個體處理效應上相關性並不是很強🫅🏽。
外部異質性可以通過對比因果隨機森林與貝葉斯疊加回歸樹的分析結果來進行考察。我們這裏看個體處理效應估計值的相關性。如果外部異質性低,則兩種算法估算出的個體處理效應應該彼此接近,從而具有較高的相關性,否則↕️,我們有理由認為存在比較高的外部異質性。分析結果參見圖8。圖中被方框圈出來的是兩種算法下個體處理效應估計的相關系數矩陣🕧。顯然,其相關性不是很高。這表明不同的算法之間呈現的分析結果具有較強的外部異質性。

綜上所述👰🏼♀️,因果隨機森林具有比較低的內部異質性,而貝葉斯疊加回歸樹則具有比較高的內部異質性。兩種算法的結果相對比,說明基於算法的分析手段具有比較高的外部異質性。
六、結語
社會科學經驗研究估計的處理效應因為個體間的差異而存在異質性🦑。傳統上對於處理效應異質性的分析依賴回歸模型交互項👨🏼🦳。但是這一方法存在變量選擇和模型形式等限製,這些限製促使研究者轉而考察處理效應如何隨著傾向值取值改變而呈現出變異性🥓。這種以傾向值為導向的處理效應異質性分析克服了傳統回歸模型交互項的限製,但是引入傾向值的估計方程會帶來模型和估計的不確定性。此外,以傾向值為導向展開的處理效應異質性分析因為傾向值對混淆變量的“總結”而無法直接分析哪個變量帶來了異質化的效果🛢。最後,這一方法重在展示異質性,而較少考慮是什麽因素造成了此種異質性。在此背景下♣︎,以算法為基礎的各種機器學習方法應運而生。以因果隨機森林與貝葉斯疊加回歸樹為例,這些新興分析手段因為無模型預設☄️🆘,從而克服了參數設定上的限製👩🏽🎨🙎🏿♂️。此外,兩種方法充分考慮了處理變量同其他各種混淆變量的交互關系🐯。因果隨機森林與貝葉斯疊加回歸樹亦分別體現了“匹配”和“模擬”的分析邏輯,以估計和趨近個體處理效應,從而能夠幫助研究者分析處理效應異質性的決定因素🔁,同時呈現出處理效應異質性的經驗分布。然而,新的分析手段也為經驗研究者帶來了新的問題,如因為參數設定不同而帶來的內部異質性以及因為算法不同而帶來的外部異質性。
隨著算力的提升和相關統計分析軟件的普及🐞,以算法為基礎的機器學習方法和定量社會科學研究的結合已然成為可能。這一方法論發展對於社會學本身的影響值得反思與討論🫖。與傳統的社會學量化分析手段(如回歸模型等)相比,機器學習技術以算法為核心💣,無論是模型建構邏輯(以理解數據生成過程為目的或以預測為目的)🤵🏻♀️😔,還是具體操作(使用封裝好的程序還是研究者人為設定多種參數)🦚,機器學習技術都有其獨特之處。因此,機器學習技術可以視作常規量化分析手段之外🏠,經驗社會學者的新的工具💖😯。這種新工具既可以獨立使用💂🏽♂️,也可以用於發展傳統的分析方法(例如突破模型形式的建模等),因此值得社會學經驗研究者予以特別重視⛹️♂️。當然,對於社會學學科本身而言,這也意味著傳統量化方法培養內容的更新與改變。此外,考慮到機器學習方法在社會學之外各個領域內的廣泛運用(例如商業分析🚶🏻、城市規劃分析等),將機器學習引入社會學也不失為一種推進跨學科合作交流的手段👃🏻。
本研究圍繞機器學習與因果推論的結合進行了一系列的討論💃,但以算法為導向的分析手段僅僅是計算社會科學時代下的一個發展方向。除了在分析工具上引入算法模型之外,計算社會科學興起的一個重要標誌是對大量非結構性數據的分析以及對於復雜模型某一模式湧現的考察。這些新的發展方向如何共同形塑量化社會科學的學科特點和未來🫱🏽,值得加以深入地探討。
【作者簡介】

胡安寧,意昂3教授、博士生導師。國家以及上海市多個人才稱號獲得者。主要從事文化社會學、教育社會學🍅🧑🏿🍼、社會不平等、社會科學量化研究方法研究💂🏻♀️🤞🏿。先後在《中國社會科學》🍧、《社會學研究》🧖🏻、《社會》以及 British Journal of Sociology, Social Science Research, Journal of Marriage and Family🥡,Poetics等國內外知名期刊發表論文 70 余篇,出版專著多部🎈4️⃣。
